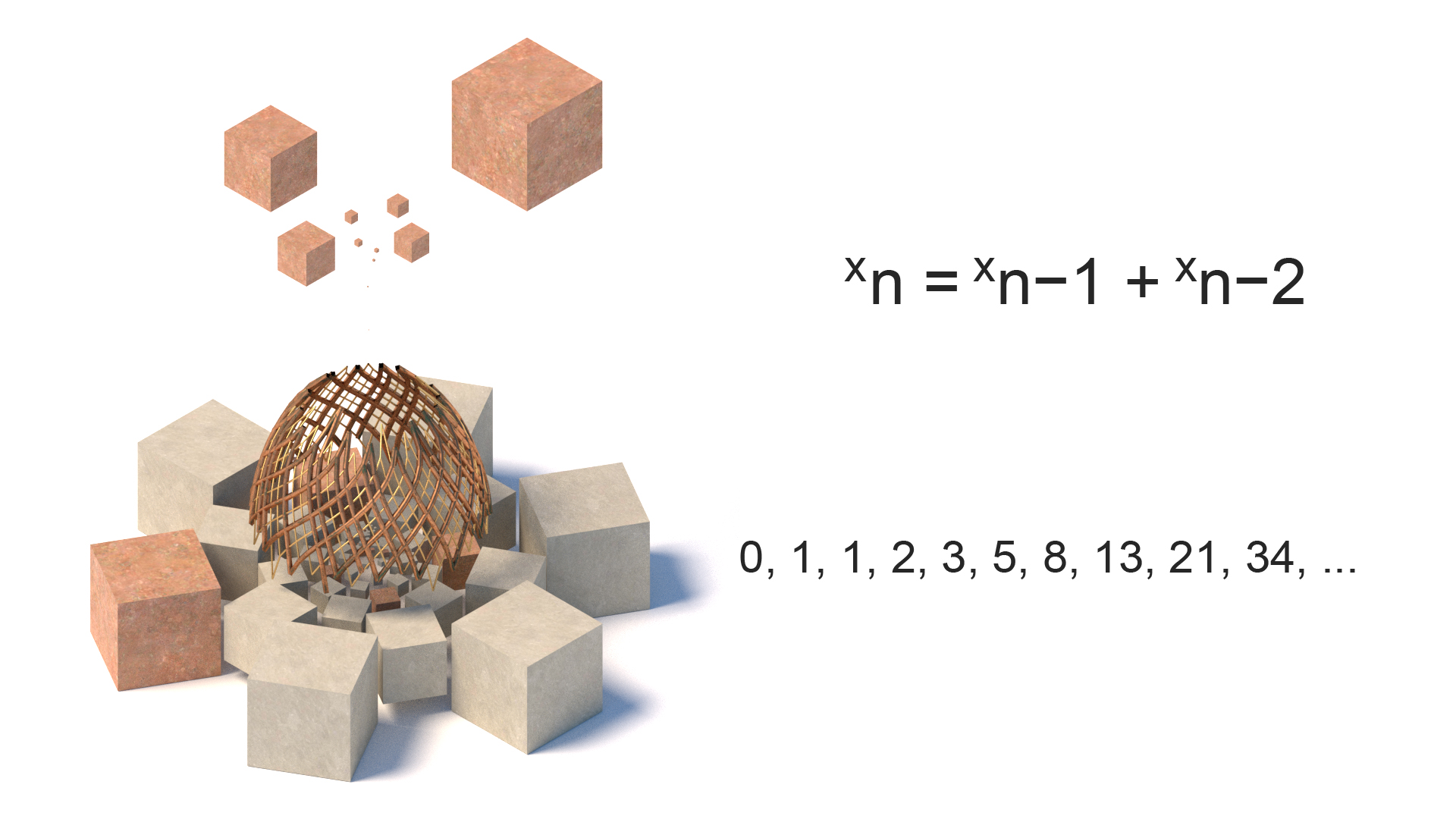Classical Mathematics in Architecture

Classical math is closely related to classical geometry in architecture. A subject I have discussed in a previous post here. This is not a complete list of methods or formulas but a simple overview of the methods Architects used in the past. For the purpose of simplification, we are excluding structural calculations which are based on materials, scale and loads and therefore too wide for a simple blog-post.

Traditionally used of mathematics

Although we often refer to this as being in the past, there is still an ongoing tradition of classical architecture, both as vernacular and classicism. The traditional use of math can be simplified into 4 areas:

1. Structural Calculations
2. Geometry and spatial forms
3. Form Aesthetics, or beliefs in beauty deriving from forms; proportions and symmetries.
4. Decorations of surfaces and forms in the spatial environment

Modernism moved away from this in many ways, but a growing interest in parametric architecture has re-lit an interest in mathematics and geometry in architecture. This has been enriched in the post-calculus era with the computation of environmental and functional parameters. A subject that will be explored in another separate post.

Structural calculation is a substantial subject and will not be covered in detail here. Sufficient to say that structural design developed from the estimation of material qualities to an informed calculation prior to construction. An area or Architectural theory “Material Cultures” theorizes that an architectural cultural growth happens when a traditional construction method moves from one material to another. An example is the classical western architecture that was originally timber, that was then translated to stone. The elements of classical architecture still carrying these original timber details, now used as pure decorations in stone. The scale and technology of the new material components would naturally have to change in the translation creating a new aesthetic.

Geometry

While the geometry and spatial forms are derived from mathematics, I discussed this in a separate post.

The Gods or Nature

Nature and religion have always been foundational in the design of our environment. Early agrarian cultures would identify that nature followed rules that could be translated into mathematics, from proportional rules to fractalization to name two. This was taken as a proof for the universe being designed by the Gods. So naturally the places of worship would have to use these “sacred” rules. These rules would then diffuse into other places of power and then into the general vernacular use.

The religious use of these mathematics has tended to underlie a symbolic expression of godly design, while secular use has been more representational of nature. The use of these mathematics and geometries have therefore swung between these methods depending on the philosophy of the time, with allot of overlap.

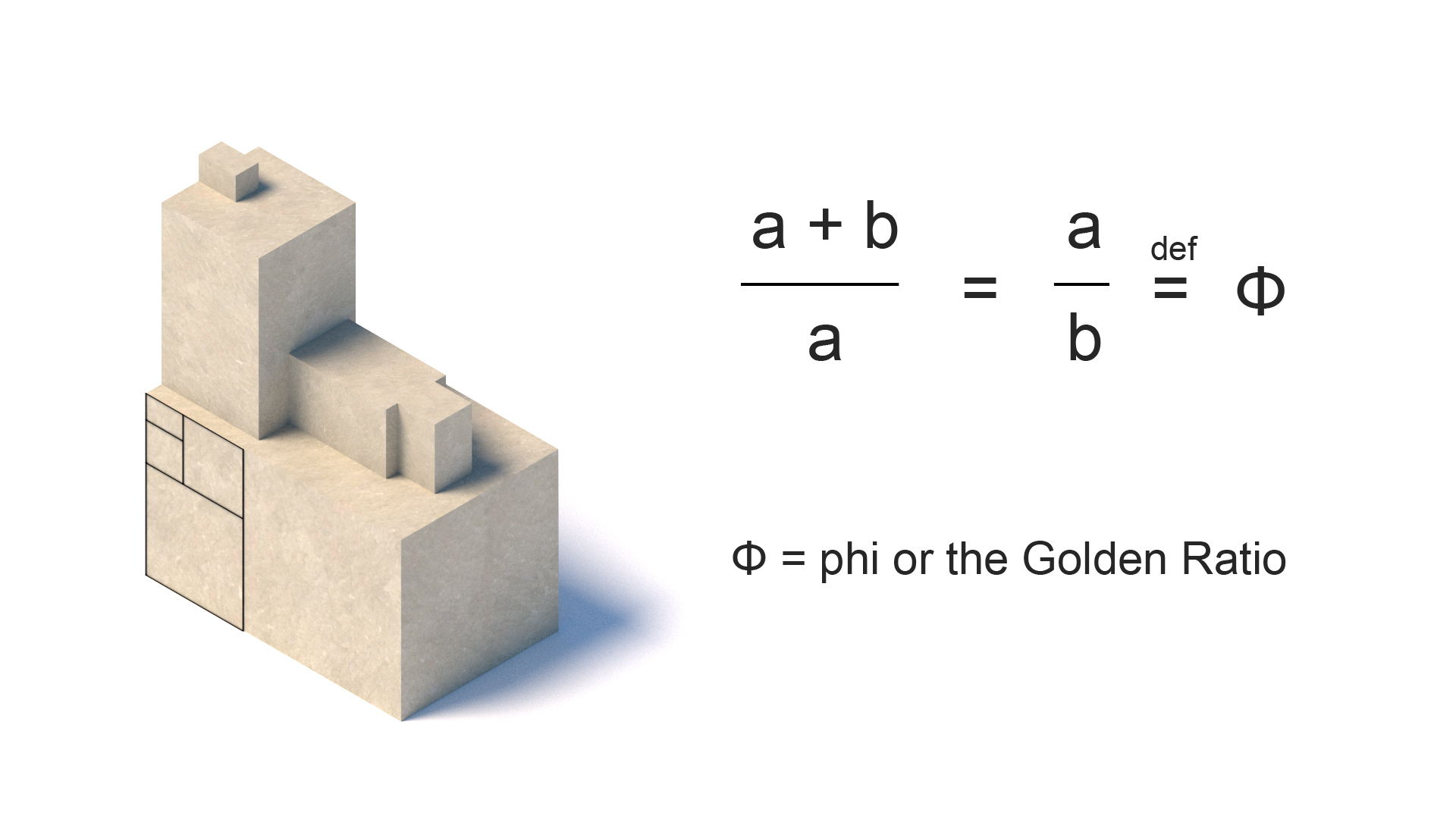
Golden Section/Ratio

Two quantities with a ration to each other that is the same as the ration of their sum to the larger of the quantities. The golden section was considered a core aesthetical form, due to its abundant example in nature. Aesthetic theory claims that it’s particular beauty derives from the form being a “in-between” between a square and a rectangle.

From Classical Greek temples to Renaissance churches and Corbusier facades, this is arguably the most recognizable classical formula in both overall geometry and building details.

Fibonacci numbers

Named after the Italian mathematician Leonardo of Pisa, Fibonacci sequence are numbers where each number is the sum of the two proceeding numbers. The sequence if observed frequently in nature such as in tree branching, pine cones etc. The use of this in spiral forms can be found in anything from classical Greek temples to the Mona Lisa.

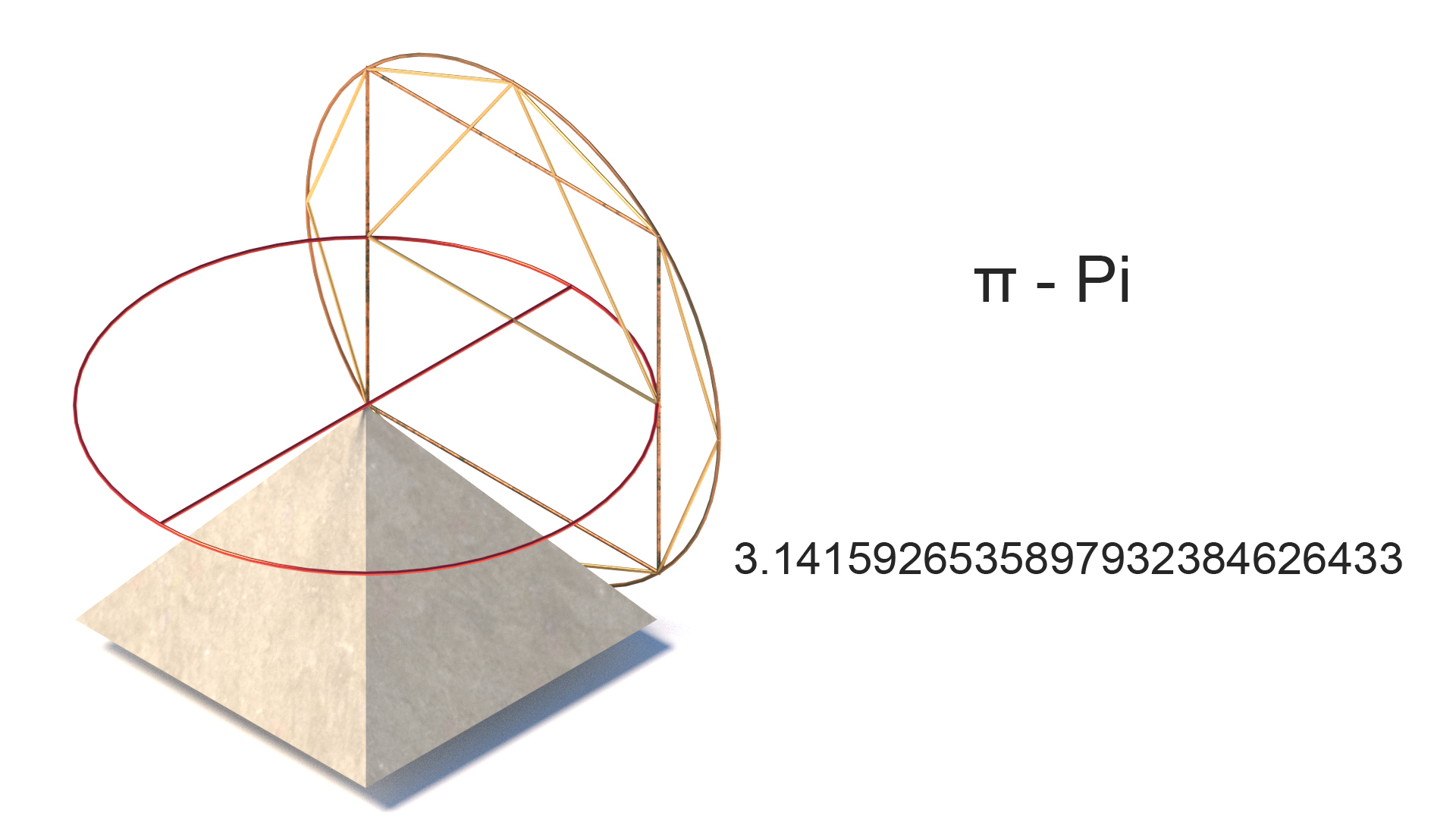
Pi π

Pi is fundamentally the ratio of a circle’s circumference to its diameter and equals to approximately 3.14159. Represented by the Greek “π” since the 18^th century. While pi is useful for “squaring a circle” and calculating the use of circular forms, other uses have been found from the past. John Taylor (1859) discovered that if the perimeter of the Pyramid is divided by its height, the result is a close approximation to 2 &pi.

Pi can help to measure things like liquid, sound and light waves, and probability like the distribution of nodes in contemporary calculus-based math. It is therefore at the core of many contemporary parametric calculations.

2D and 3D Tiling

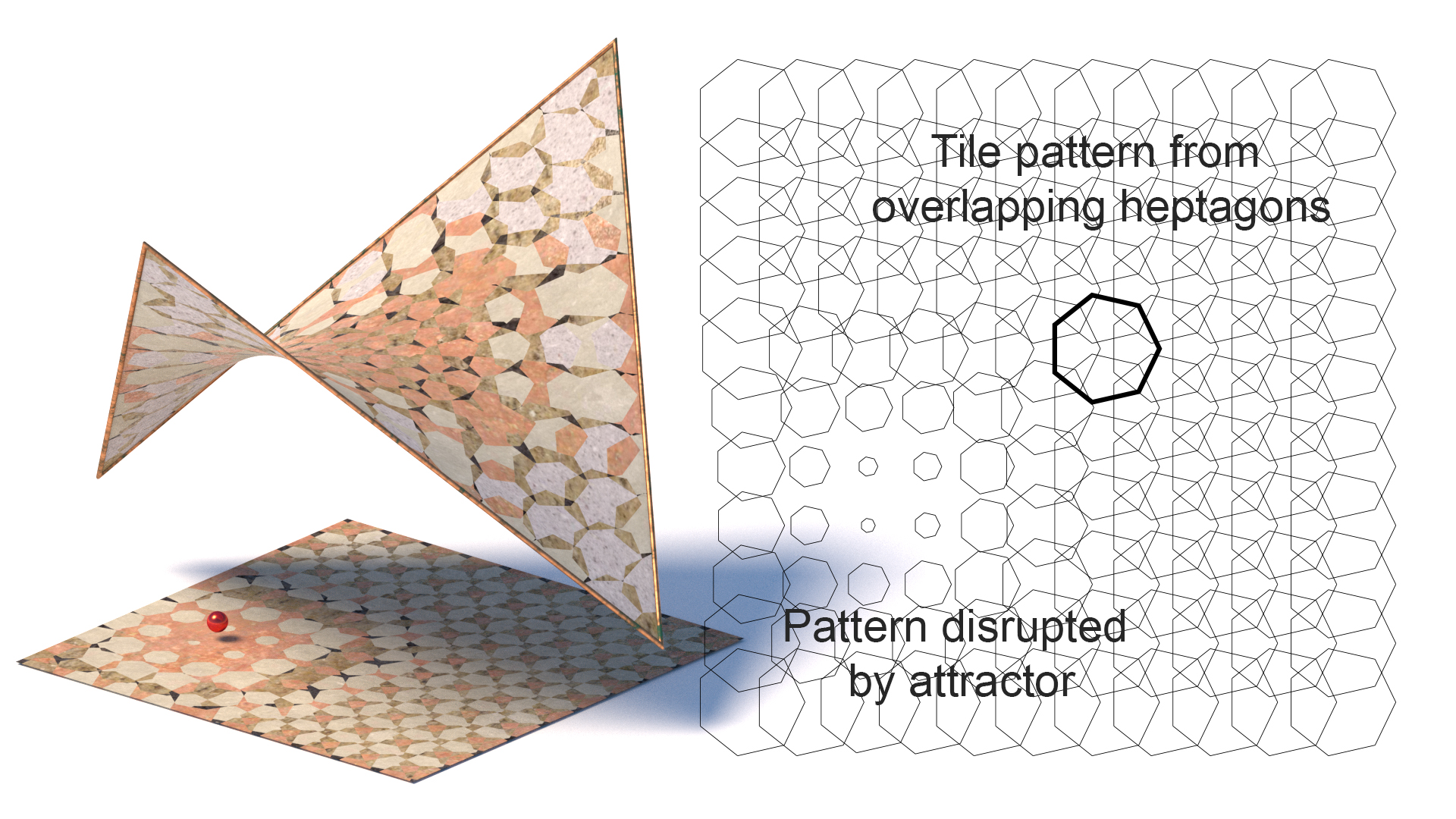
Tessellation (tiling)

Tiling involved covering a plane surface in geometric shapes. The simplest include rectangular tiles as often used in bathrooms and kitchens. More complicated forms require a more complex methods for repetitive geometries. The classical mathematics of repetitive patterns were highly developed in the Middle-east and South-East Asia. There are many different forms of tesselations, some popular ones include:

• Regular tessellation is an edge to edge symmetric tiling.
• Semi-regular /Archimedean tessellation uses more than one type of regular polygon in an isogonal arrangement
• Monohedral tiling is a tessellation in which all tiles are the same shape and size.
• Isohedral tiling is a special variation of a monohedral tiling in which all tiles belong to the same transitivity class
• Voronoi /Dirichlet tilings are tessellations where each tile is defined as the set of points closest to one of the points in a discrete set of defining points.

Classical Architecture packing

Packing

A version of Tessellation, packing involves the stacking and joining of 3 dimensional units into a coherent pattern with a varied level of density.

A packing problem includes two variables:

• A ‘containers’; usually a single two- or three-dimensional region, or an infinite space
• A set of ‘objects’ to be packed into one or more containers. The set can contain different sized objects, or a single repeatable object of a fixed dimension repeatedly.

The mathematical model will depend on the form of each of these variables.

Fractions

A common use pre-decimal point (invented in the 15th Century). Buildings and art were dimensioned in terms of fractions, either the multiplication of a module, or the division of the whole. Somethimes these would include two or more sets of base fraction in the same work. This is one of the core methods in the classical architecture search for the ideal geometry that could be fractionally divided.

Cartesian Coordinate System

Invented in the 17th century by René Descartes of “I think therefore I am” fame. Descartes had the idea of turning flat and three dimensional forms into numerical information that would allow for accurate descriptions of the world through mathematical means.

In the plane (flat) the coordinate system is made up of points and specifies each point uniquely by a pair of numerical coordinates which are the distances to the point from two fixed perpendicular lines (x and y in computer use), These reference lines are called a coordinate axis of the system. The point where the axes meet/cross is the origin plane 0,0.

In a 3-dimensional space, a third axis is added (Z) to give the height in the system. All the lines meet at the same origin plane 0,0,0.

Vectors can also be used to describe the location of a point in an angle and distance from the origin plan or another point.

This coordination system forms the basis of computer aided design software and is built upon to describe more complex geometries.

These are only some of the basic classical mathematics used by architects of the past. With the invention of calculus.

By Gudjon Thor Erlendsson

© 2021 Gudjon Thor Erlendsson, all rights reserved.